Operations & Structs¶
The Operations layout is defined by the External API type you choosen in the Interface tab. We'll explain the available options for each type in this section.
REST¶
Operations¶
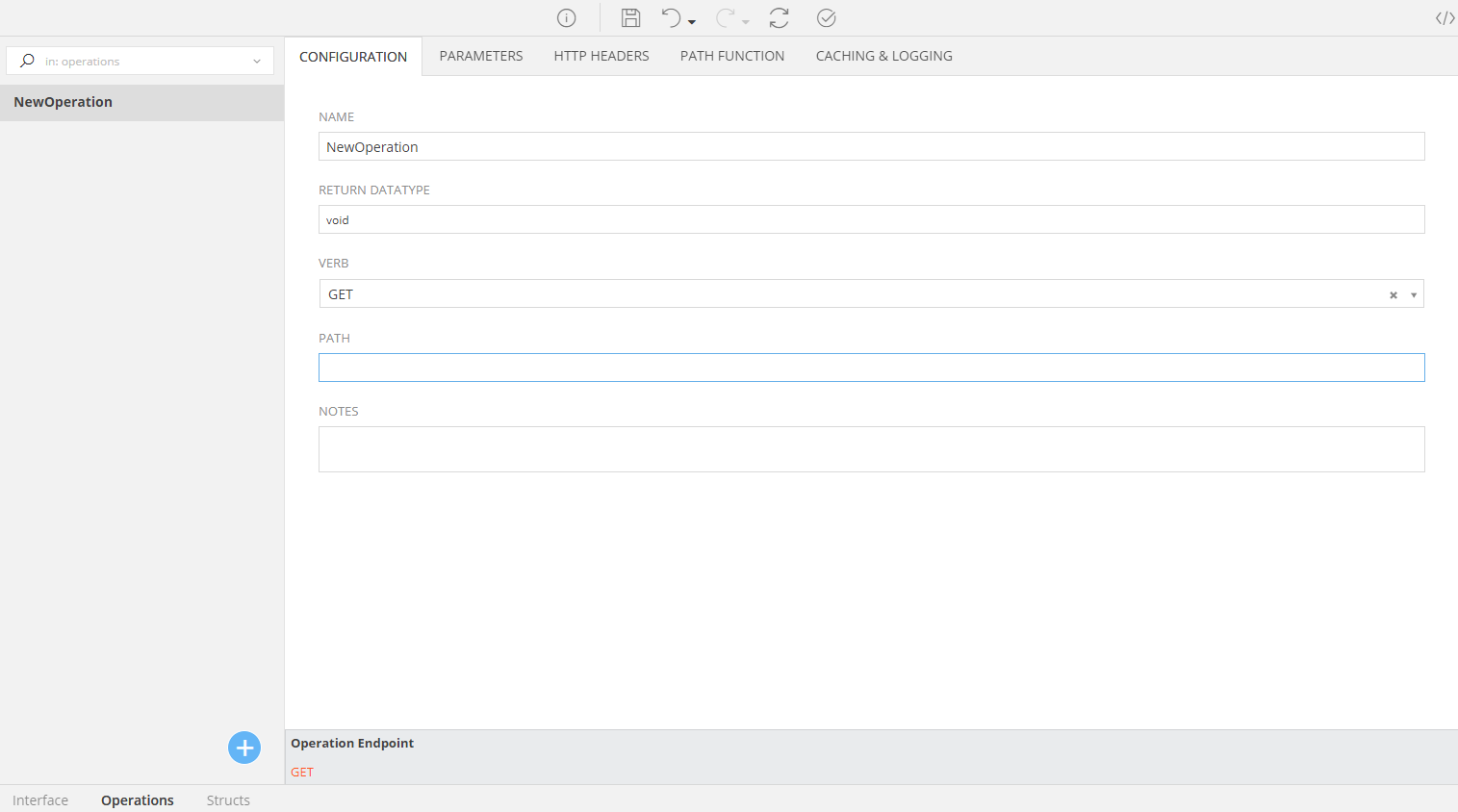
New Operation¶
To add a new Operation go to the 
button and add a New Operation. The following layout will appear:
On the left part of the screen you can switch between the Operations you create by selecting them. You can also use the search panel to easyly find the Operation you want. The right part of the screen contains 5 tabs for configuring your Operation according to the endpoint's specifications.
Configuration Tab¶
Here you set the most basic properties for the API endpoint you want to integrate:
| Property | Description |
|---|---|
| Name | This is the name of your current operation |
| Return Datatype | This is the return datatype of the API response. You can use any Class or Struct you have defined in your project |
| Verb | The type of the HTTP request that this Operation is accepting. You can choose between GET, PUT, POST and DELETE |
| Path | The endpoint path for the current Operation. It can be seen at the bottom of the current tab |
| Notes | Notes that can help the developer remembering and maintaining the service |
Parameters¶
In this tab you can define any parameters needed by your Operations. To Add one or more Parameters (when and where needed), simply
- Click on the Add... link
- Select its DataType
- Select its Type (i.e. QueryParameter for URIs such as http://myAPI.com/countries/name={parameter} )
- Give it a Default Value, if none is passed
- Add some Notes to let your Team understand what this parameter is for
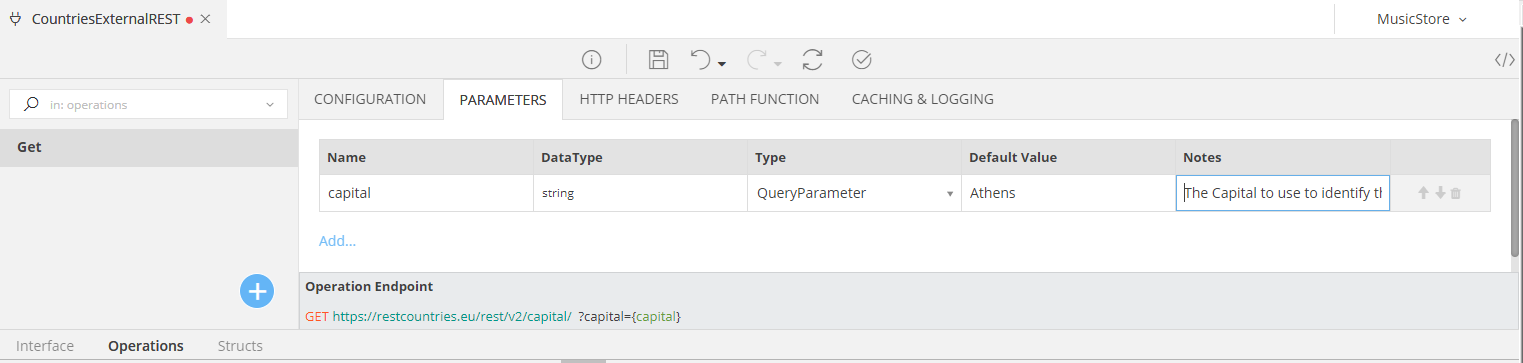
Example: Query Parameters¶
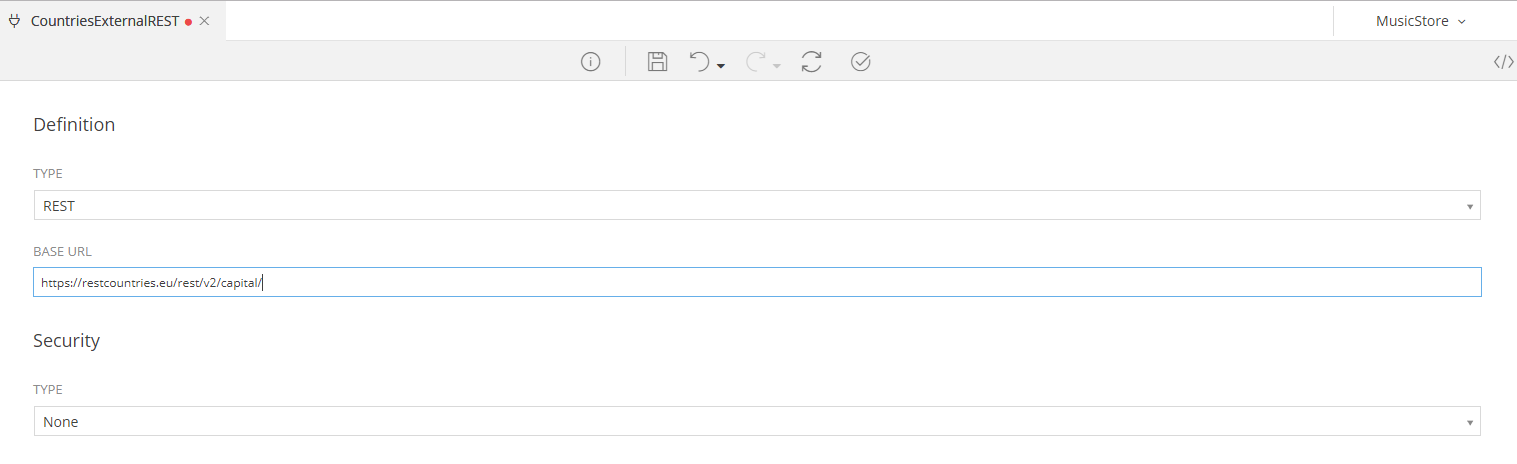
Say that you need to hit a Service to get Information on a Country, based on its Capital. A nice REST Service to choose for this task would be: https://restcountries.eu/rest/v2 and the GET Operation you would hit would be: https://restcountries.eu/rest/v2/capital/{capital}
Thus, the REST Definition would look like this:
and since its GET Operation requires the user to pass the "Capital", so as to search for the Country, the Operation's Parameter would be
- a
string - set as a QueryParameter
You can define as many parameters you need to successfully call a REST Service, with any types you require (e.g. primitives for QueryParameters, entire Objects or Collections for RequestBodies etc).
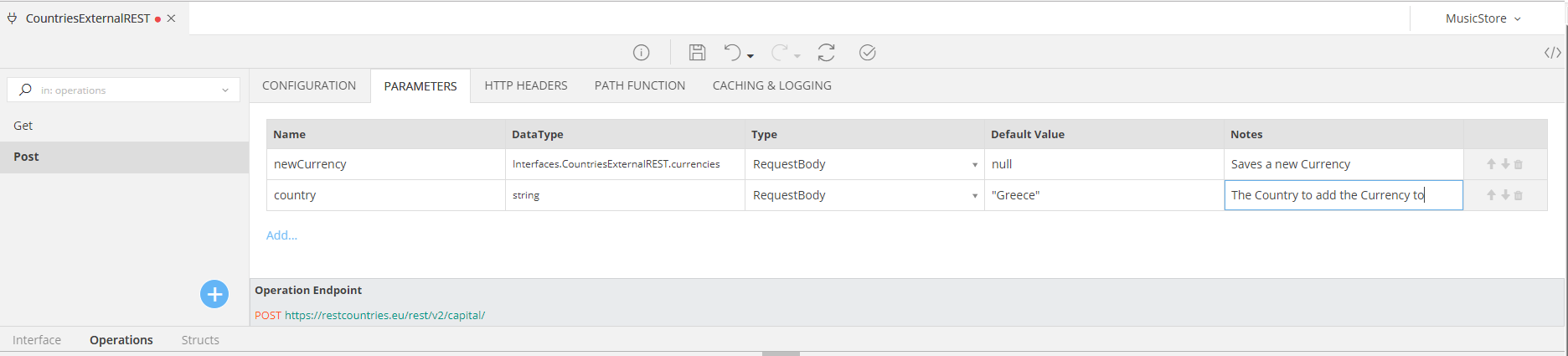
Example: RequestBody Parameters¶
The following example shows a POST Operation that adds a new Currency to a Country (note: it does not exist in the REST Service mentioned before. It is a fake URI created solely for this example!).
It expects a string as the Country that will receive a new Currency, as well as a currency Object, obtained by the REST Service itself and defined (automatically) as its struct.
HTTP Headers¶
In case HTTP Headers are required by the API operation, they can be added in the Headers tab. To add a header, simply
- Click on the Add... link
- Set its name
- Set its value
Attention
Header Value must be proper Mamba code. If you want to assign a hardcoded string value, "myValue" must be typed. Typing just myValue (without double quotes) will result in a validation error.
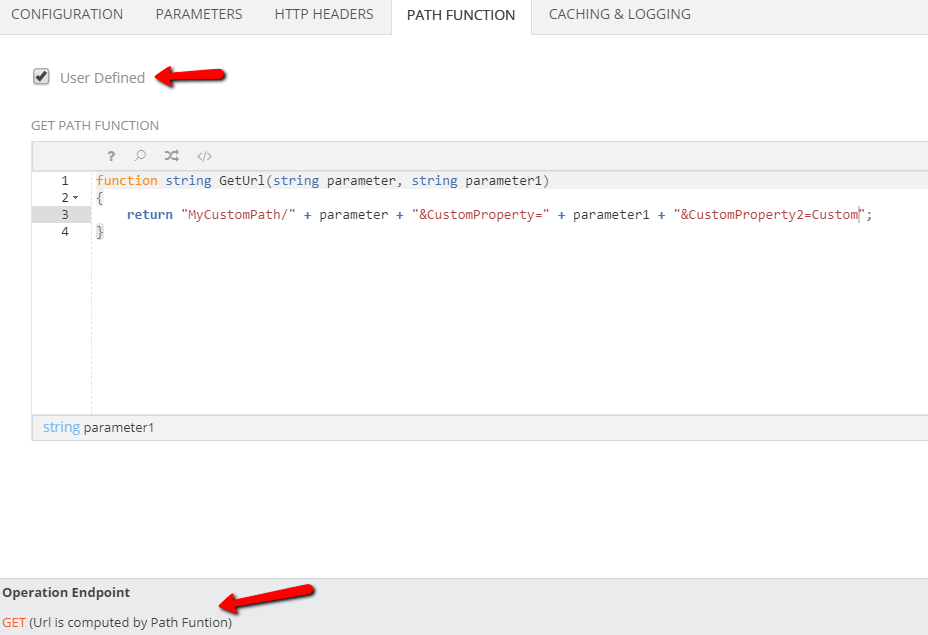
Path Function¶
By default, the Operation Endpoint url is autogenerated based on the Path defined in the Configuration tab and on the Parameters that are defined as UriPart or Query Parameter.
There are cases where you may want to have full control over the Endpoint Path. To do this, check the User Defined check box. A code editor appears where you may write a Mamba function that must return a string, using the operation parameters as input arguments. This string will be used as the operation end point path.
Caching & Logging¶
Caching¶
If enabled, this option uses a Cache (either an internal, or an external, if defined, such as a Redis Server) that will hold your External API's responses, so that if a response is cached, it will be instantaneously retrieved from the Cache, this eliminating the need to issue another API call.
There are a few Options that can be defined per API Call Operation, namely:
- Whether or not the Cached Items should be held per user or in a more global manner
- Whether or not the Cache should abide by the Default Cache Settings set in the Configuration of the Application, or be more tailored to the API Operation they are set for
Logging¶
If enabled, the execution of the API Operation will be logged, keeping information such asa
- Who executed the API Operation
- From which IP Address
- Which was the outcome of the execution
Structs¶
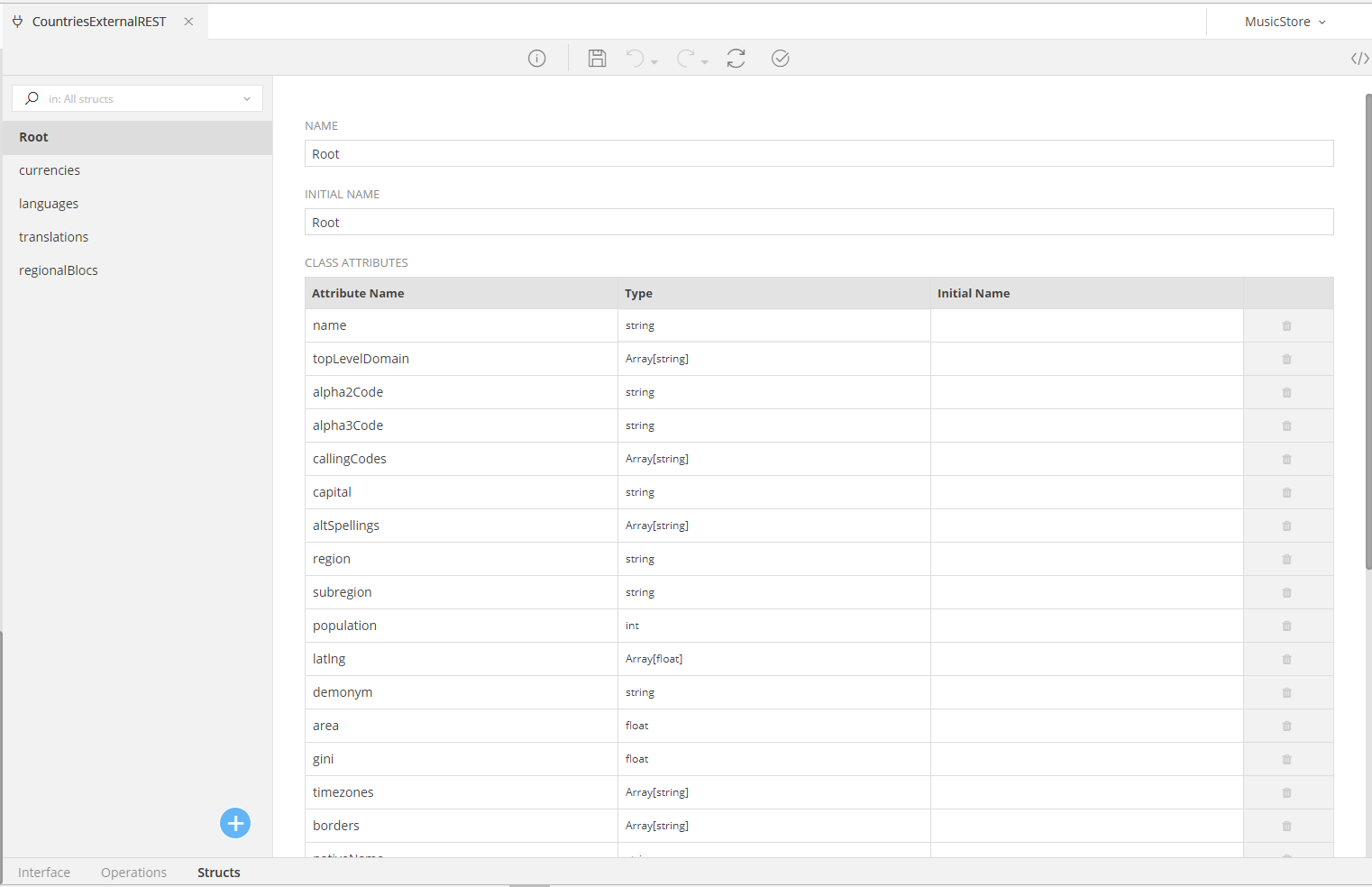
As soon as you define your REST API Endpoint and refresh the Model, zAppDev will execute the underlying operations, collect their structs (in terms of input parameters and/or result types) and populate the Struct Tab with the detected classes and their relationships.
For example, the Countries API described before will detect the following structs, starting with the Root, that is the parent of all other structs:
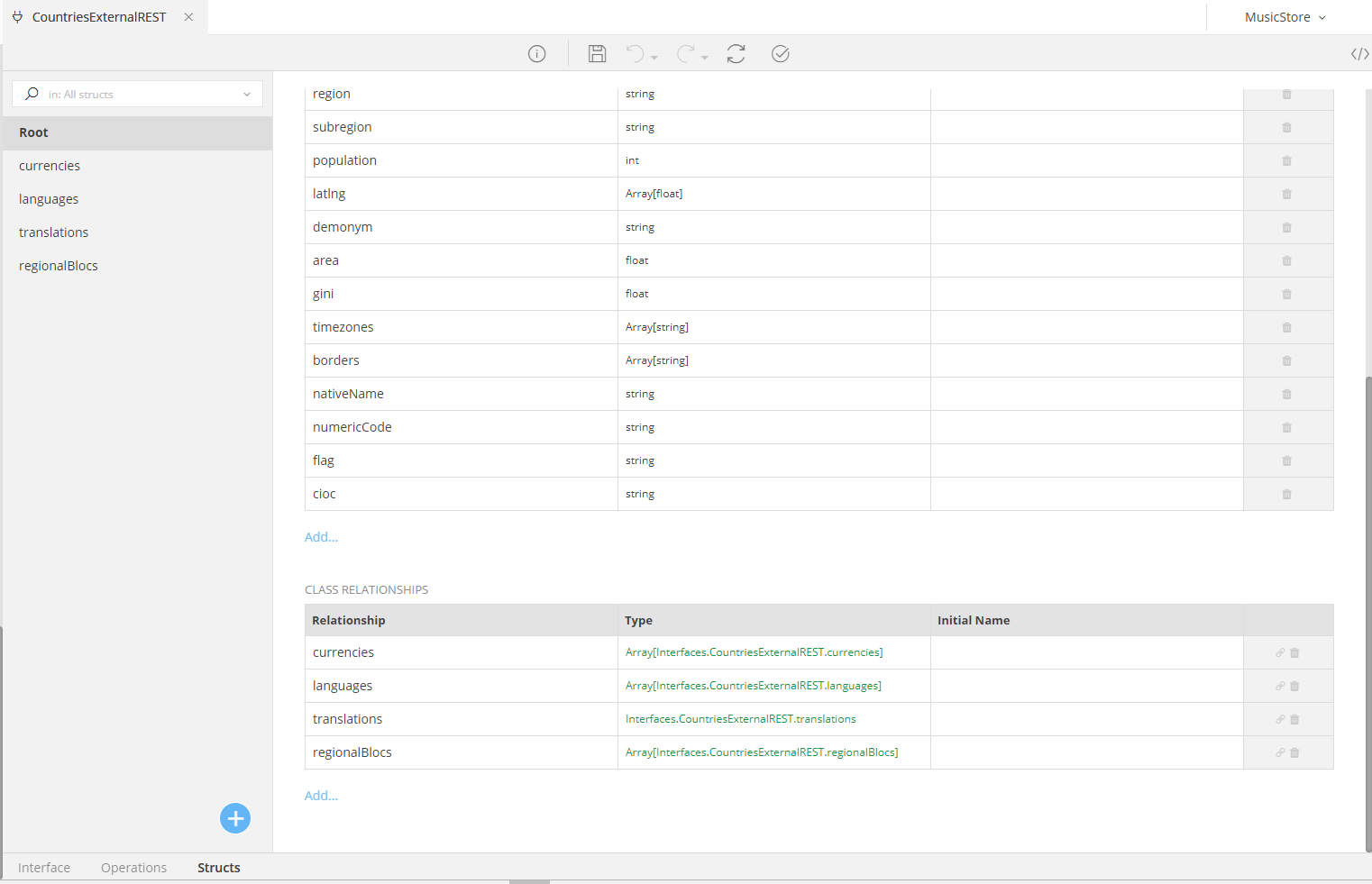
Additionally, since (in this example) the Root (top most) struct is related to other structs, such as currencies, languages, translations and regionalBlocs, its Relationships will also be automatically populated, giving a result similar to the following:
Every Struct has the same configuration items:
| Property | Description |
|---|---|
| Attribute Name | This is the name of the Attribute inside the Struct. You can change it if you want (e.g. give it an alias) however you MUST define its initial name in the Initial Name configuration |
| Type | This is the Data Type of the Attribute |
| Initial Name | In case you changed the name of the Attribute (to an Alias, for example), here you must define the original name it had before the change |
SOAP¶
Operations¶
The Operations of a SOAP Service are automatically created with all of their underlying settings, as soon as you select your SOAP Source and hit refresh. Contrary to the REST Services described earlier, a SOAP Service cannot be altered in terms of Operations and/or Parameters, since they are created following the instructions of the WSDL structure. You can, however, define their Caching & Logging settings, just as described in the REST Services documentation
Configuration Tab¶
Here you set the most basic properties for the API endpoint you want to integrate:
| Property | Description |
|---|---|
| Name | This is the name of your current operation. |
| Return Datatype | This is the return datatype of the API response. |
| Notes | Notes that can help the developer remembering and maintaining the service |
Attention
You will see that the Properties described are editable. However, we would advice you against changing them, unless you really-really know what you are doing and why. The best practice would be to leave them follow the structure of the WSDL fetched by your SOAP service.
Parameters¶
This tab presents the parameters used by each of the SOAP Service Operations. You can add and delete them, however since they have been prepopulated by the SOAP Service's definition, make sure you know what you are doing and, more importantly "why", before you change them.
Caching & Logging¶
The Caching and Logging options for the SOAP Services are same with the ones described during the REST API. For more information, read this
Structs¶
As soon as you define your SOAP Endpoint and refresh the Model, zAppDev will download the WSDL file, parse its definition, collect its structs (in terms of input parameters and/or result types) and populate the Struct Tab with the detected classes and their relationships.
From then on, you will be able to configure and use them following the same logic described here
Library¶
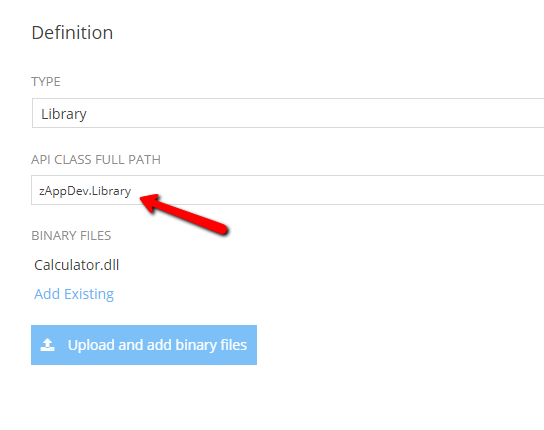
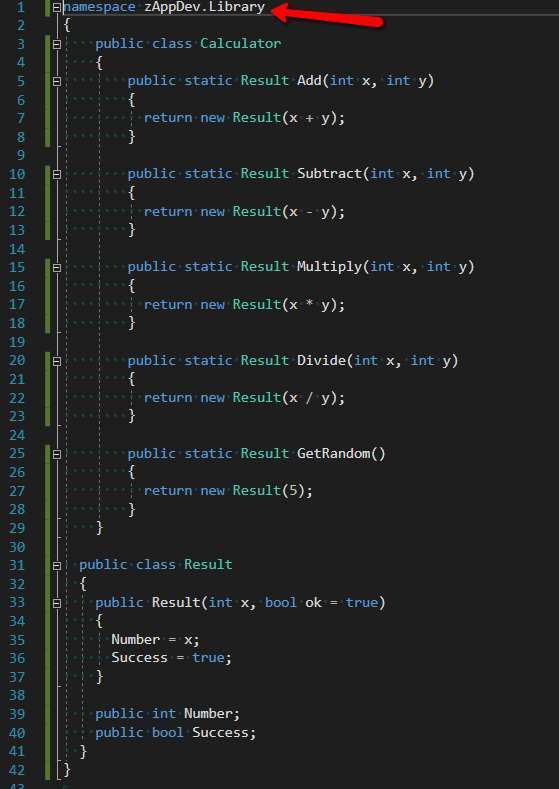
Library type APIs are the way to extend zAppDev's functionality using existing libraries. To define a Library API you only have to upload the related binary file(s) and set the API class full path.
Attention
It is important that Api Class Full Path, matches the namespace defined in the binary file.
Operations¶
To add a new Operation go to the button and add a New Operation.
The following layout will appear:
Configuration Tab¶
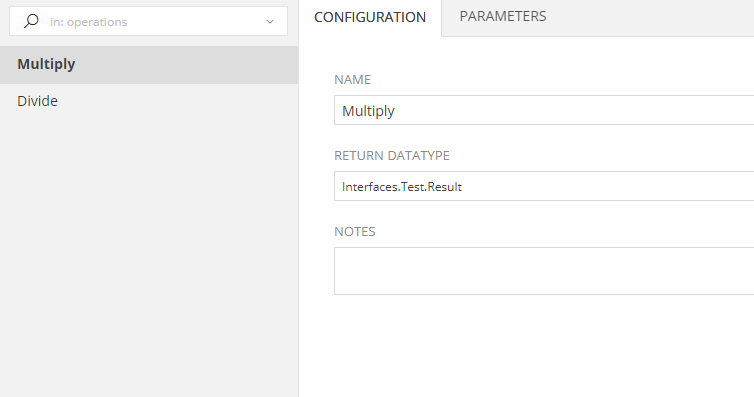
As with any other Service, here you set the most basic properties for your API Endpoint:
| Property | Description |
|---|---|
| Name | This is the name of the method. Must match the one defined in the Library. |
| Return Datatype | This is the return datatype of the Library method. You can use any Class or Struct you have defined in your project |
| Notes | Notes that can help the developer remembering and maintaining the service |
Attention
It is important that the operation is defined both as public and static in the Library
Parameters Tab¶
In this tab you must define the parameters in order to ** exactly match the signature** of the Library method, in terms of name and DataType. To Add one or more Parameters (when and where needed), simply
- Click on the Add... link
- Select its Name
- Select its DataType
- Give it a Default Value, if none is passed
- Add some Notes to let your Team understand what this parameter is for
Structs¶
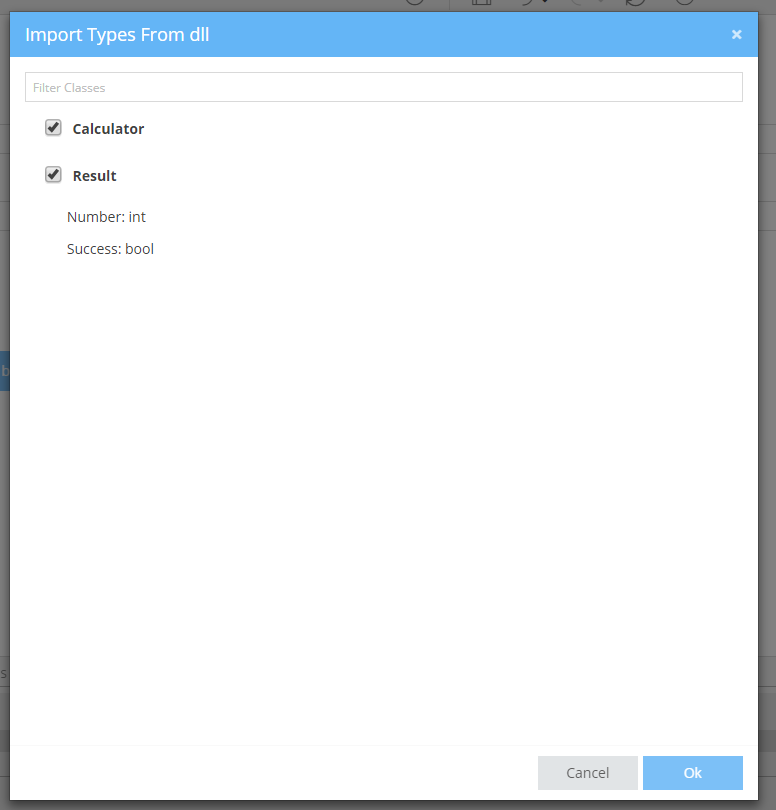
To import structs, click the Refresh button on the Ribbon. zAppDev will autodetect the classes defined in the Library and populate the Struct Tab with the ones user has selected.
From then on, you will be able to configure and use them following the same logic described here
XSD¶
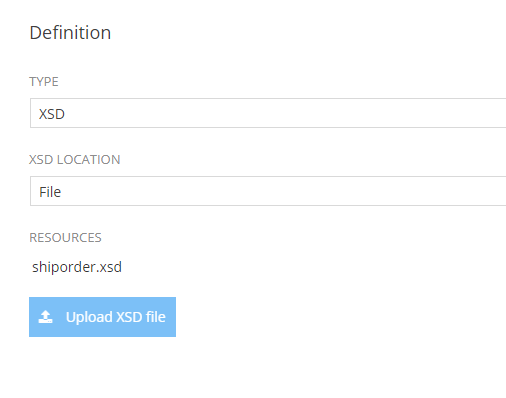
zAppDev is able to handle data stored in xml documents via XSD APIs. You may define an XSD type API by uploading a single XSD file or a zip containing multiple XSD files.
Operations¶
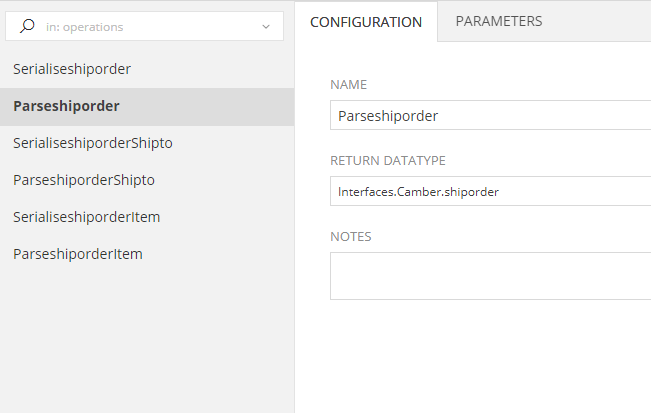
The Operations of an XSD API are automatically created with all of their underlying settings, as soon as you fill-in the Configuration tab and hit refresh and cannot be altered. For each struct defined in the XSD, a Parse and a Serialize method is created.
Parse method can be used to parse xml string content into the corresponding struct.
Serialize method can be used to serialize a struct into xml.
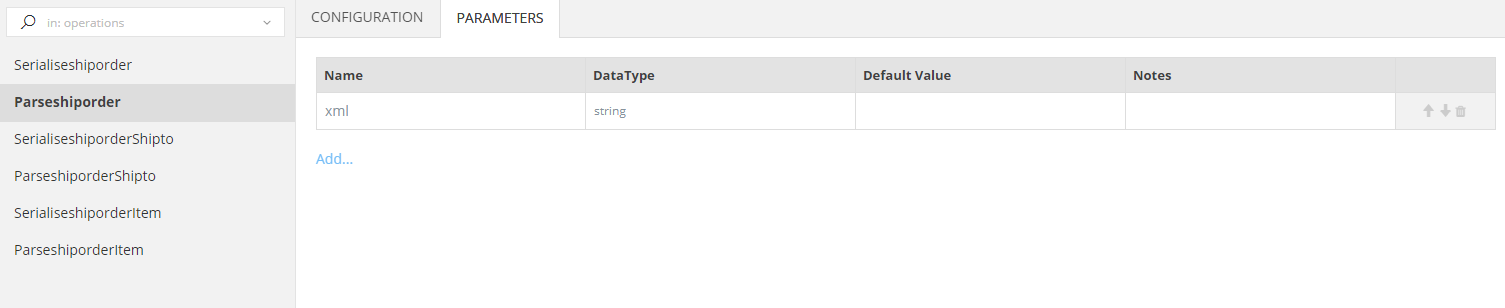
In the Parameters tab you may review the parameters of the above mentioned methods. You are allowed to alter them, but again this will be usefull in extremely rare cases.
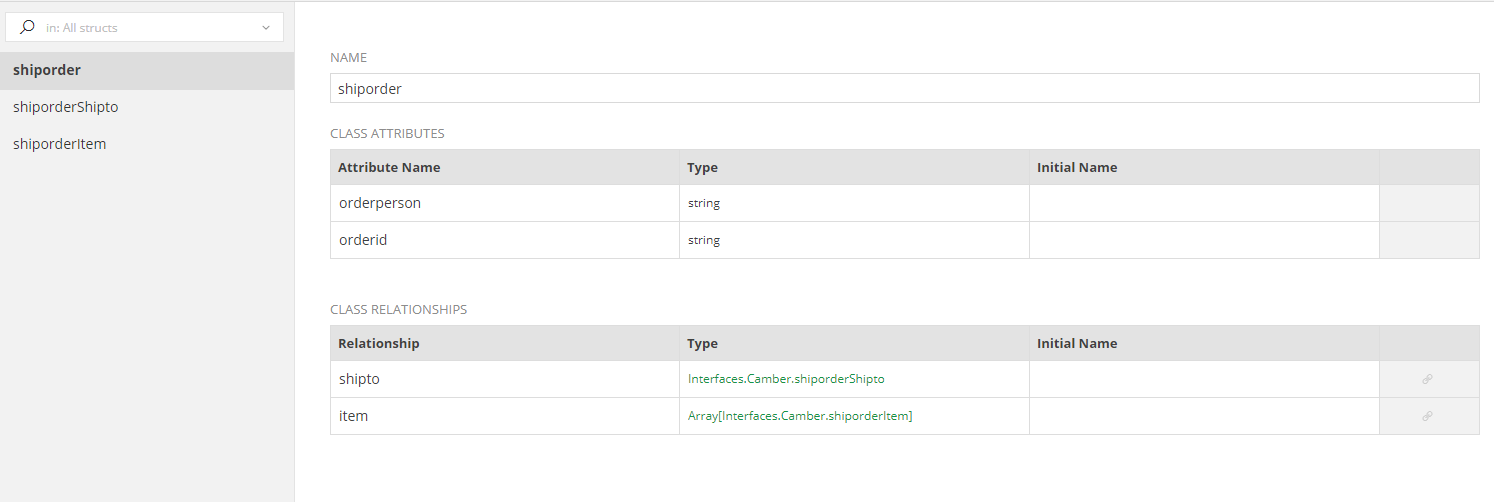
Structs¶
The Structs Tab is autopopulated with the classes and relationships defined in the XSD file(s). They cannot be altered except from defining Initial Names for special cases that have been mentioned before.
Application Database¶
Operations¶
To add a new Operation go to the button and add a New Operation.
The following layout will appear:
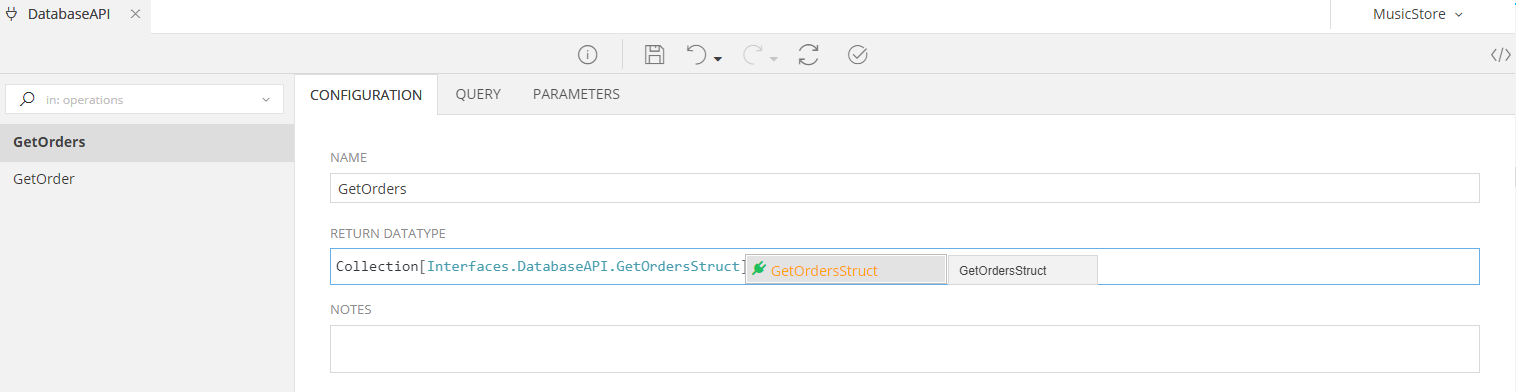
Configuration Tab¶
As with any other Service, here you set the most basic properties for your API Endpoint:
| Property | Description |
|---|---|
| Name | This is the name of your current operation |
| Return Datatype | This is the return datatype of the API response. You can use any Class or Struct you have defined in your project |
| Notes | Notes that can help the developer remembering and maintaining the service |
Hint
We would advice you to first define the Struct of your Database API Operation and then define its Return DataType
Query Tab¶
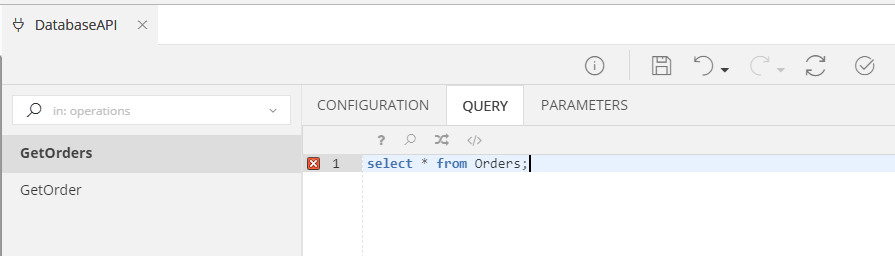
In the Query Tab you can define the select query that your Operation should execute.
Attention
The Query must always return a resultset (i.e. SELECT). Other queries that do not return anything (e.g. DELETE) should not be written there
As soon as you define your SQL Query, zAppDev will run it and populate its Parameters and Structs
Parameters Tab¶
If the SQL Query ran in your Operation contains parameters, they will be automatically defined in this tab. You can alter, add and remove them if you wish; remember, however, to update your Query as well, so that the SQL Query and the Parameters defined are aligned.
Example: Operation with no Parameters¶
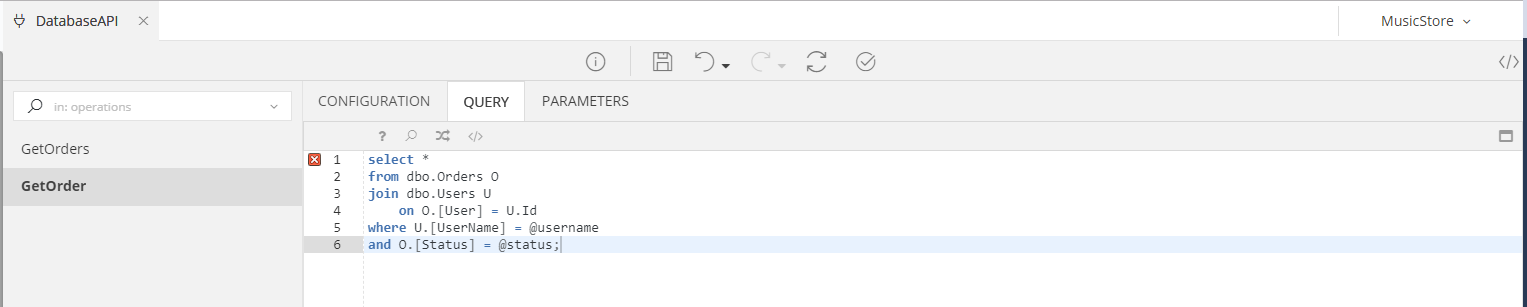
Example: Operation with Parameters¶
The image that follows shows an Exposed API Operation that consists of a Query expecting two parameters:
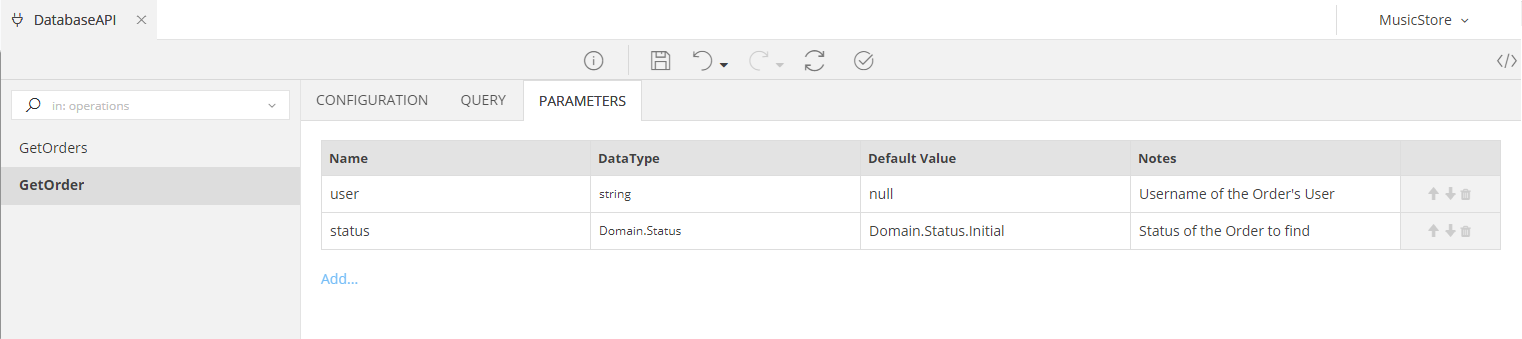
The two parameters will be added to the Parameters tab, allowing you to define their expected Datatype, Default Value and Notes
Attention
Make sure that the parameters inside your Query (marked with an @) and the ones you see in the Parameters Tab are the same, in terms of their variable names. For example, the @user parameters used in the Query must be the same in the list of the Parameters. Should you rename them in one place, propagate that change in the other as well.
Structs¶
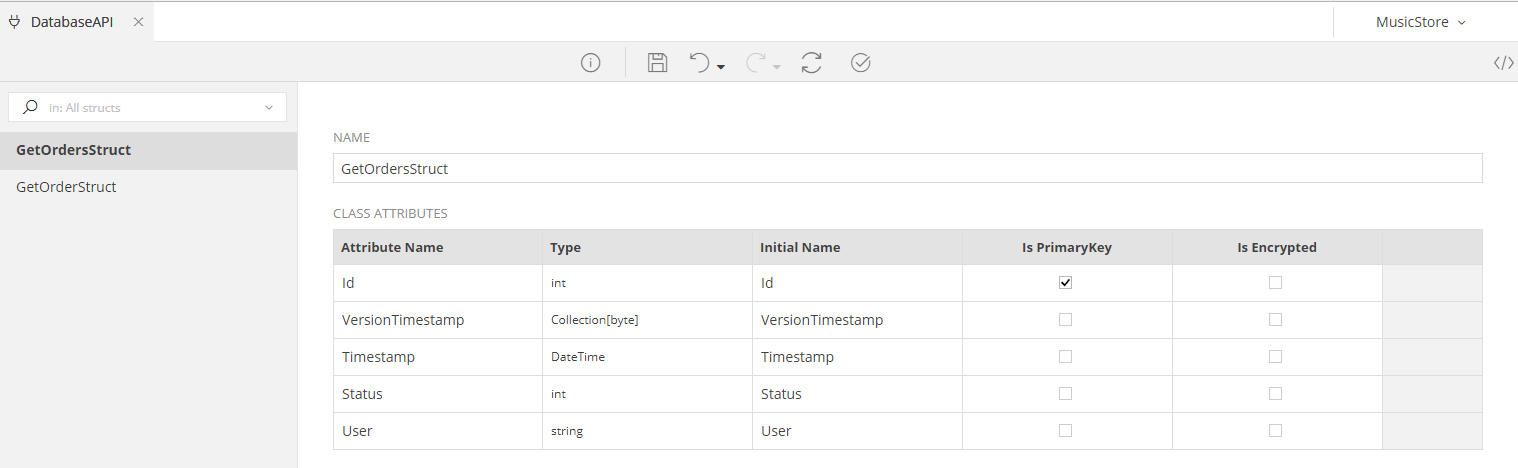
As soon as you define the SQL Query to be ran on any Operation, zAppDev will run it, detect its result and populate the Structs Tab following the resultset it got. For example, the GetOrders SQL Query shown before, will have a Struct looking like this:
Attention
If you rename a Struct, remember to reset the Return DataType of any Operation that uses that Struct
